Summer School on

Graphs in Computer Graphics, Image and Signal Analysis

Rutsker, Bornholm, Denmark, August 14-19, 2011

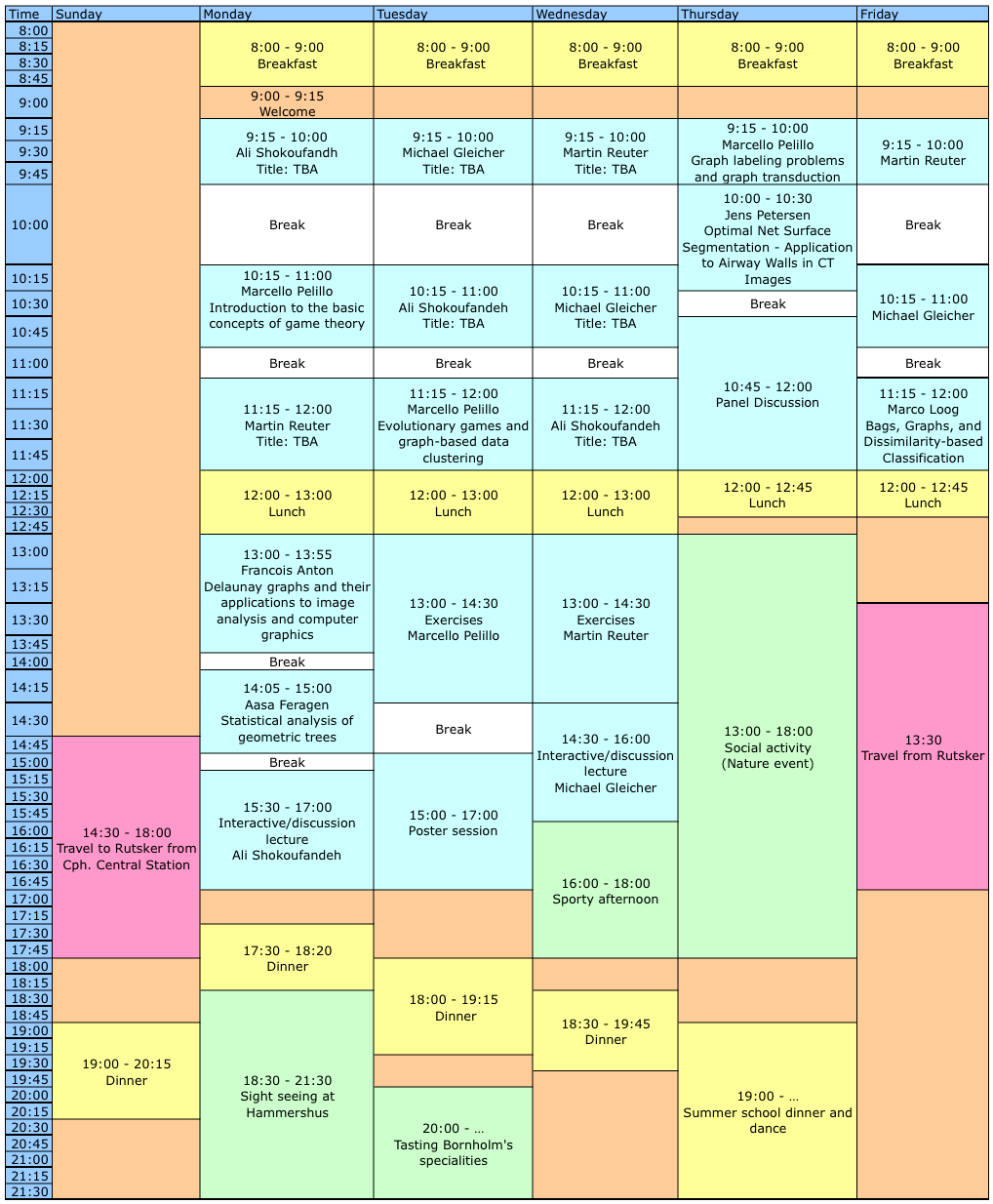
Program

The program is available as pdf here

The summer school will contain lectures and exercises mainly covered by the four invited speakers. Local speakers will provide examples of graph-based methods in their research and relate the topic to the research at DIKU and DTU Informatics. In addition to the scientific program there will be social activities including outdoor events Wednesday afternoon and the summer school dinner Thursday evening.

Invited lecturers

Ali Shokoufandeh

Ali Shokoufandeh will be introducing the basic definitions of graphs as well as provide an overview of algorithmic graph theory; this will cover a diverse range, from basic topics and simple algorithms to more advanced topics, including shock graphs for shape matching.

In his Second lecture, he will talk about the geometry of graphs and an overview of basic results related to embedding graphs into metric spaces. He will discuss how basic embedding techniques can be used for solving the sparsest cut and flux minimization problems. He will continue this lecture by covering topics in spectral graph theory and their applications to graph matching, and image segmentation problems.

In his third lecture, Ali will talk about approximation algorithms and using semi-definite programming techniques for solving a variation of hitting sets known as the canonical set problem. He will discuss the applications of canonical sets to 3D view-based object recognition and image feature selection problem. A high-level formulation of the problem using nonlinear optimization will be followed by the overview of techniques for approximating the canonical set problem. Sample experimental results will conclude this lecture.

The topic of Ali Shokoufandeh's final lecture will be on the use of embedding techniques for graph matching problem. He will discuss how graphs can be embedded into geometric spaces, reducing the many-to-many graph matching problem to a weighted point matching problem, for which efficient many-to-many matching algorithms exist.

Slides:

  1. Lecture 1: Graphs: Introduction
  2. Lecture 2: Embedding and Spectrum of Graphs
  3. Lecture 3: Canonical Sets in Graphs
  4. Lecture 4: Many to Many Matching in Graphs

Suggested reading material:

  • M. Fatih Demirci, Yusuf Osmanlioglu, Ali Shokoufandeh, Sven J. Dickinson: Efficient many-to-many feature matching under the l1 norm. Computer Vision and Image Understanding 115(7): 976-983 (2011)
  • M. Fatih Demirci, Ali Shokoufandeh, Sven J. Dickinson, Yakov Keselman, Lars Bretzner: Many-to-Many Feature Matching Using Spherical Coding of Directed Graphs. ECCV (1) 2004: 322-335
  • John Novatnack, Trip Denton, Ali Shokoufandeh, Lars Bretzner: Stable Bounded Canonical Sets and Image Matching. EMMCVPR 2005: 316-331
  • M. Fatih Demirci, Ali Shokoufandeh, Yakov Keselman, Lars Bretzner, Sven J. Dickinson: Object Recognition as Many-to-Many Feature Matching. International Journal of Computer Vision 69(2): 203-222 (2006)
  • M. Fatih Demirci, Bram Platel, Ali Shokoufandeh, Luc Florack, Sven J. Dickinson: The Representation and Matching of Images Using Top Points. Journal of Mathematical Imaging and Vision 35(2): 103-116 (2009)
  • Frans Kanters, Trip Denton, Ali Shokoufandeh, Luc Florack, Bart M. ter Haar Romeny: Combining Different Types of Scale Space Interest Points Using Canonical Sets. SSVM 2007: 374-385
  • Trip Denton. 2007. Subset Selection Using Nonlinear Optimization. Ph.D. Dissertation. Drexel University, Philadelphia, PA, USA. Advisor(s) Ali Shokoufandeh. AAI3259958

Martin Reuter

Laplace-Beltrami Eigenstuff

Martin Reuter will be talking about the Laplace operator and its properties, useful in many different applications. He will describe the relationship between the graph Laplacian, the mesh Laplacian and the FEM approach, which can be extended to higher order approximations. For the mesh and FEM approach surfaces or volumes are represented as simplices that may be understood as nodes/points connected by edges, i.e. graphs with additional geometric information. The Laplace-Beltrami operator (Laplace operator on manifolds) can be applied to these discretization, allowing for accurate computation of Eigenvalues and Eigenfunctions of the represented shapes. These spectral values are isometry invariant and therefore important in many applications dealing with non-rigid shapes such as shape matching, shape analysis and segmentation/correspondence.

Practical examples include statistical shape analysis of subcortical structures in the human brain between diseased and healthy subjects.

Slides:

  1. Lecture 1: Background
  2. Lecture 2: Computation
  3. Lecture 3: Applications

Exercises

The exercises will be in Matlab and deal with the computation and application of spectral entities for triangle meshes. If you like bring some meshes (in OFF format, 2D manifolds with no boundary) to play with.

  1. Exercise slides and accompanying Matlab files (tar)
  2. Matlab script with solutions

Useful links:

  1. OFF format documentation can be found at http://www.geomview.org/docs/html/OFF.html
  2. Martin Reuter's shape DNA software http://reuter.mit.edu/software/shapedna/
  3. Shape retrieval contest with links to several shape databases http://www.itl.nist.gov/iad/vug/sharp/contest/2011/NonRigid/

Suggested reading material:

Marcello Pelillo

Game Theory in Graph-Based Computer Vision and Pattern recognition

The development of game theory in the early 1940's by John von Neumann was a reaction against the then dominant view that problems in economic theory can be formulated using standard methods from optimization theory. Indeed, most real- world economic problems typically involve conflicting interactions among decision-making agents that cannot be adequately captured by a single (global) objective function, thereby requiring a different, more sophisticated treatment. Accordingly, the main point made by game theorists is to shift the emphasis from optimality criteria to equilibrium conditions. As it provides an abstract theoretically-founded framework toelegantly model complex scenarios, game theory has found a variety of applications not only in economics and, more generally, social sciences but also in different fields of engineering and information technologies. In particular, in the past there have been various attempts aimed at formulating problems in computer vision, pattern recognition and machine learning from a game-theoretic perspective and, with the recent development of algorithmic game theory, the interest in these communities around game-theoretic models and algorithms is growing at a fast pace.

The goal of this short course is to offer an introduction to the basic concepts of game theory and to provide an overview of recent work on the use of game-theoretic models in graph-based computer vision and pattern recognition problems.

Slides:

  1. Lecture 1: Introduction to game theory
  2. Lecture 2: Evolutionary games and graph-based data clustering
  3. Lecture 3: Graph labeling problems and graph transduction

Exercises

At the end of the first lecture, the class will be asked to split in sub-groups each of which will be assigned a short paper, related to the contents of the course, to read and comment. To make the study more profitable and active, in the final part of the exercise slot, scheduled for the second day, a representative from each group will be asked to provide a mini-presentation (around 5 minutes) of the assigned paper.

Suggested reading material

Michael Gleicher

Motion Synthesis By Example

Michael Gleicher will give lectures on motion graphs, with the foundations of human movement synthesis for animation, on which he has done a considerable amount of work. This has become the dominant approach over the past decade. Michael Gleicher will give three lectures organized as follows:

First lecture will give an overview of the problems of motion synthesis, with a focus on application in computer games. The idea would be to motivate the idea of "synthesis by example" and to introduce the basic building blocks of most approaches: concatenation (graphs) and blending.

In his second lecture Gleicher will give an introduction to Motion Graphs, with some of the details and issues (like how matching is performed). Match webs and match graphs, linking together different motion sequences, will be treated. Also ideas of blending-based synthesis will be described. (in the style of Kovar&Gleicher 2002)

In his third and final lecture a survey of some of the more advanced approaches built on these basic building blocks are presented. Parametric Motion Graphs that show how graphs and blending can be put together will be presented. The talk lecture will also touch upon recent work in the field on making more effective use of graphs, improving control, and avoiding explicit graphs altogether. (e.g. the Motion Fields work at Washington) (Heck&Gleicher, Shin&Oh)

Slides:

  1. Lecture 0
  2. Lecture 1: Introduction: Synthesis-By-Example
  3. Lecture 2: Motion Graphs
  4. Lecture 3: Parametric Graphs & Open Questions

Exercises

Michael Gleicher will talk about the foundations of motion synthesis: character representations and rotations, how signal processing ideas connect to motions, etc. This session will aim at giving the students insights with rotations and kinematics. Students are also expected to gain basic intuitions on foundations such as rotation vectors, matrix logarithm, exponential coordinates, quaternions, etc.

Slides:

  1. Blending
  2. Foundations

Suggested reading material:

Local lecturers

Aasa Feragen

Geometric trees are combinatorial trees with an additional geometric structure, such as branch length or branch shape. Geometric trees appear, for instance, as airway, vessel or dendrite trees in medical images, in protein folding or as phylogenetic trees describing the development of species. In this talk, we shall outline the properties of a desired statistical framework for analyzing such trees, and describe three different state-of-the-art approaches to defining such statistical theories for tree-structured data. We shall focus on the mathematical modeling aspects and geometric intuition of the three approaches rather than on theory, and discuss the pros and cons of all three methods. The talk will not require prior knowledge, but the main references are included below for the enthusiastic reader.

Slides: Statistical analysis of geometric trees

References:

  • L. J. Billera, S. P. Holmes, and K. Vogtmann. Geometry of the space of phylogenetic trees. Advances in Applied Mathematics, 27(4):733-767, 2001.
  • H. Wang and J. S. Marron. Object oriented data analysis: sets of trees. Annals of Statistics, 35(5):1849-1873, 2007.
  • A. Feragen, S. Hauberg, M. Nielsen, F. Lauze: Means in spaces of treelike shapes, ICCV 2011.

Jens Petersen

The use of optimal net surface segmentation methods has been growing within medical image segmentation the last couple of years. The methods can find the globally optimal solution of multiple surfaces in multiple dimensions using surface cost functions and a wide range of geometric constraints in polynomial time using maximum flow algorithms. In this presentation the methods along with an application to human airway walls in CT images will be demonstrated.

Slides: Optimal Net Surface Segmentation - Application to Airway Walls in CT Images

References:

  • X. Wu and D. Chen. Optimal Net Surface Problems with Applications Automata, Languages and Programming, Vol. 2380, pp. 775-775, 2002.
  • J. Petersen, M. Nielsen, P. Lo, Z. Saghir, A. Dirksen and M. de Bruijne. Optimal graph based segmentation using flow lines with application to airway wall segmentation. Information Processing in Medical Imaging, pp. 49-60, 2011.

Marco Loog

Marco Loog works with Pattern Recognition Laboratory, Delft University of Technology and The Image Group, University of Copenhagen

He will present joint work with Wan-Jui Lee, Veronika Cheplygina, David Tax, and Bob Duin. Pattern Recognition Laboratory, Delft University of Technology.

Dissimilarity-based classification bridges the gap between between classification techniques using feature-based pattern recognition and machine learning and those based on structural approaches. Attributed graphs contain structural as well as feature-based information and can be considered a generalization of representations employed in so-called multiple instance learning--or multiset classification--on the one hand and of purely structural representations on the other. In my lecture, I will introduce the basics of the dissimilarity approach to classification. Subsequently, I will discuss the extreme cases of multiset and structural classification and their generalization through attributed graphs. Finally, I will provide some, maybe toyish, examples that demonstrate the performance improvements possible by combining the two extremes.

Slides: Bags, Graphs, and Dissimilarity-based Classification

References:

  • R. Bunke. Graph Classification Based on Dissimilarity Space Embedding, S+SSPR 2008, Lecture Notes in Computer Science, 2008.
  • Lee, Cheplygina, Tax, Loog and Duin. Bridging Structure and Feature Representations in Graph Matching. International Journal of Pattern Recognition and Artificial Intelligence, submitted, 2011.
  • Pekalska and Duin. The Dissimilarity Representation for Pattern Recognition. World Scientific, 2005.
  • Sørensen, Loog, Lo, Ashraf, Dirksen, Duin and de Bruijne. Dissimilarity-Based Quantification of Lung Disease from CT, MICCAI 2010, Lecture Notes in Computer Science, 2010.
  • Tax, Loog and Duin. Bag Dissimilarities for Multiple Instance Learning, SIMBAD 2011, Lecture Notes in Computer Science, 2011.

Francois Anton

Delaunay graphs were introduced in Anton's Ph.D. thesis. They play a fundamental role in the construction of generalised Voronoi diagrams and in many different application areas, including homotopy continuation, cartography, GIS, GPS, robotics, material science, bioinformatics, crystallography and image analysis and computer graphics. We will present their definition, their properties, their relationships with the medial axis and the skeleton, as well as their applications in image analysis and computer graphics. The extension of homotopy continuation using barycentric coordinates based on a Delaunay graph plays a central role in some of the most recent applications.

Slides: Delaunay Graphs and their applications to Computer Graphics and Image Analysis

References:

Posters

Andreas Kårsnäs - Learning histopathological patterns

Mads Ingerslew Ingwar - Find the Five Differences

Ole Thomsen Buus - Analysis of Seed Sorting Process by Estimation of Seed Motion Trajectories

Sara Sharifzadeh - Conditional Random Fields for Multispectral Data Analysis

Dan R. Jørgensen - Finding Discriminative Regions that Optimally Separate Healthy and Osteoarthritis Knees

Anders B. Beck - Spacio/Temporal Situation Assessment for Mobile Robots

Signe Thorup - 2D Single Image Super-Resolution

Deo Musiige - RF Power Consumption Emulation Optimized with Interval Valued Homotopies

P. A. Dufour - Automatic Segmentation of Intraretinal Layers from Optical Coherence Tomography Images

Rasmus Ramsbøl Jensen - Removing that Annoying Hair g Growth!

Sudhakar Tummala - Diagnosis of OA by Automatic Quantification of Incongruity from Knee MRI

Gopal Karemore - Anatomic Breast Coordinate System for Mammogram Analysis

Program for the summer school:

(Graph image)

Summer School on Graphs in Computer Graphics, Image and Signal Analysis
Rutsker, Bornholm, Denmark, August 14-19, 2011
Dina Riis Johannessen dinariis@diku.dk