Graphs
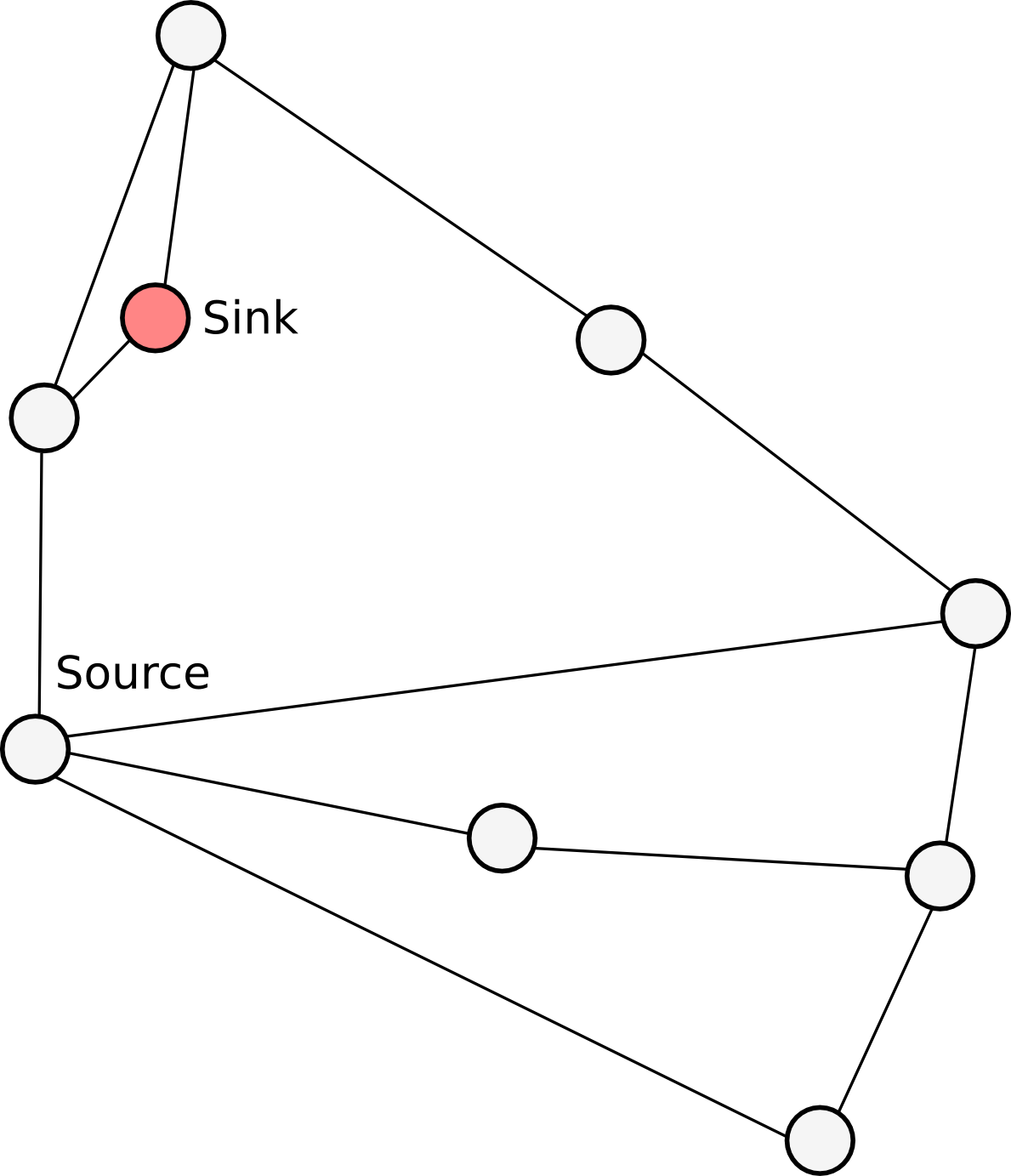
Graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A graph refers to a collection of vertices or nodes and a collection of edges that connect pairs of vertices. The graph structure can be visualized as illustrated in the figure to the right.
Clearly, this definition of graphs leaves room for designing different specialized graph structures, suitable for a whole range of purposes. The next section describes some of the popular structures that will be treated by the invited speakers at the summer school.
The subsequent section describes some of the analysis that is commonly applied to these structures, with an emphasis on methods that will be treated at the summer school.
Graph structures
From the basic notion of graphs a lot of different graph structures have been proposed and investigated that will be discussed on the summer school. Graphs may have special patterns, and may be generalized in numerous ways.
Useful graph structures (i.e. both special symmetries and useful definitions) include
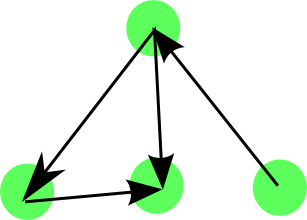Graphs can be directed or undirected.
In a directed graph (shown right) each edge has a direction, and we distinguish between edges with different directions.
These may, among others be used to model information flows. Unless stated otherwise, trees and graphs are assumed undirected.
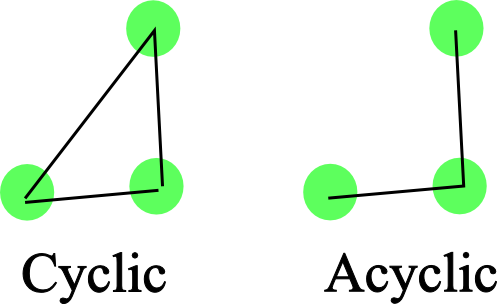Cyclic and acyclic graphs
If a graph is cyclic we can find a closed path (or closed walk) in the graph. Identifying paths with different properties has spawned a huge amount of research.
Cliques
Cliques are densely (fully) connected subgraphs in a bigger graph
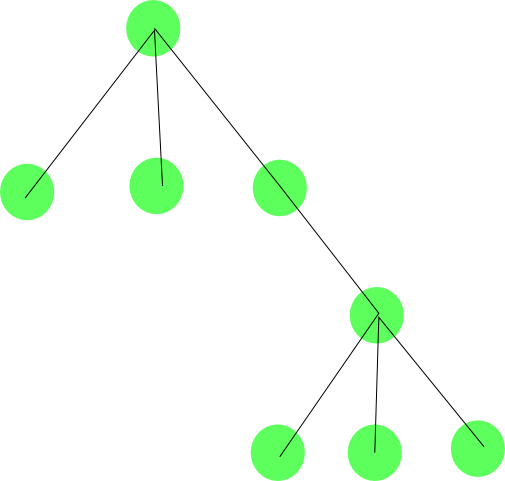Forest and Trees
In graph theory a forest is an acyclic graph, and a tree is a connected acyclic graph; thus a forest may consist of a set of trees. If a tree is undirected, any node can be assigned as the root of the tree. Clearly, this structure is well suited for hierarchically organized data or methods.
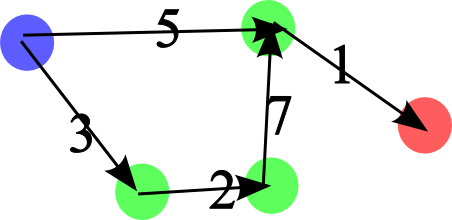Weighted graphs.
Graphs in which the edges are assigned weights - also termed networks.
Vertices may also be assigned values, and particularly source and a sink can also be assigned, and this structure has been used with great success for graph cut algorithms.
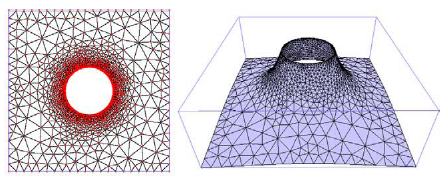Graph embedding.
Graphs may be embedded in spaces or on manifolds, and in this space the graph has non-intersecting edges. A special case of embedding is a triangulated surface, and a tetrahedral representation of a volume.
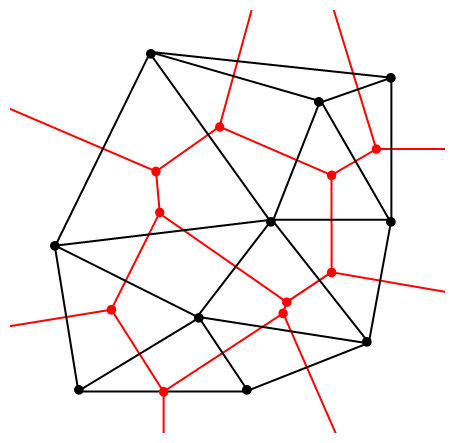Dual graphs
A dual graph is a graph which has a vertex for each plane region of an embedded graph, and an edge for each edge in the graph joining two neighboring regions. The term "dual" is used because this property is symmetric. The Voronoi diagram and the Delaunay triangulation are dual graphs of one another. The notation of duality is also valid for embeddings of graphs on manifolds.
Hypergraphs
Higher order similarities and hypergraphs describes relationships that are not only associated with two vertices, both more. In hypergraphs edges may connect sets of nodes instead of just one node to another node. If a hypergraph has only edges that each has k vertices it is called k-uniform.
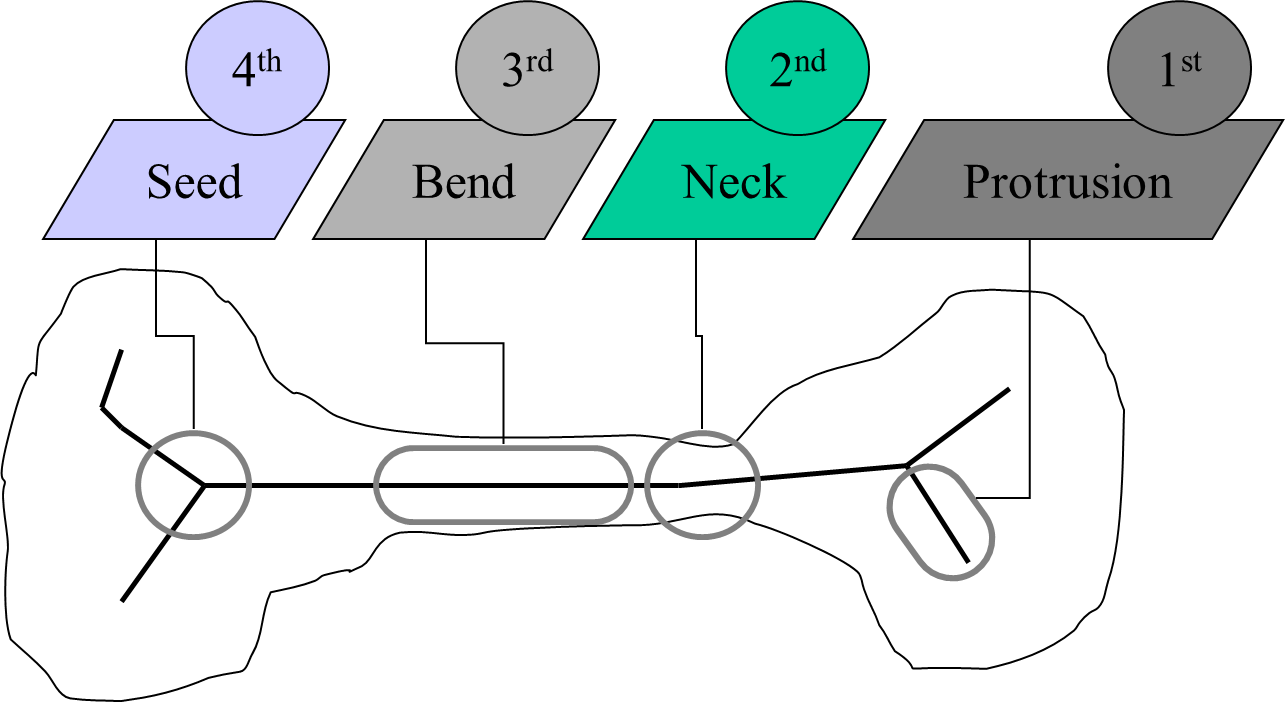Shock graphs
Shock graphs are derived from skeleton models of shapes, and focus on the properties of the surrounding shape. The different points on the skeleton are labeled according to the shape, and noted as a vertex, and the vertices are connected to form a graph. The graph is subsequently split by copying nodes, to form a tree, and the shock tree has been shown to be suitable for shape matching.
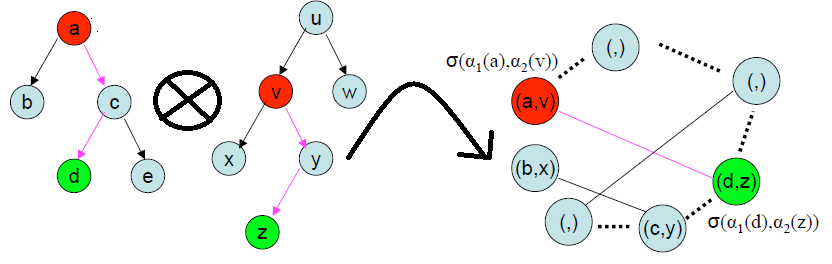Tree association graph
In a tree association graph, pairs of vertices from each tree are associated to each other, with a weight, if they (can) have similar parent/child relation in both trees. When the weights measure goodness of fit, the clique with the biggest cumulated weight, denotes the biggest matching subtrees.
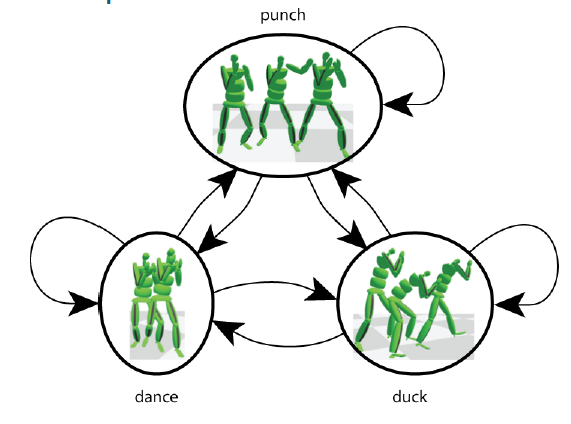Motion graphs
A motion graph is a collection of several motion spaces, and the edges describe how transitions can be made between the different spaces.
Graph analysis
The graph structure has spawned many ways to do analysis of graphs, several of which will be presented at the summer school.
- The distribution and sizes of cliques (e.g. the maximal clique) are in some cases important features of graphs.
- Graphs may correspondingly reveal clustering (many problems can be simplified by dividing things up in a reduced number of clusters).
- Graph distance measures can be used to compare graphs which may again be used for graph matching (this is highly useful if one has graph-based representations of objects and one wants to compare these).
- The shortest path may reveal the optimal solution to a problem.
- Spectral graph theory can be used to analyze shapes represented by triangle sets for patterns or for matching.
- Graph matching.
- All-pairs shortest path (Floyd-Warshall).
- Network flow.
- Network optimization.
