Syllabus
| From shapes to manifolds | ||
|---|---|---|
| Rasmus R. Paulsen | ||
|
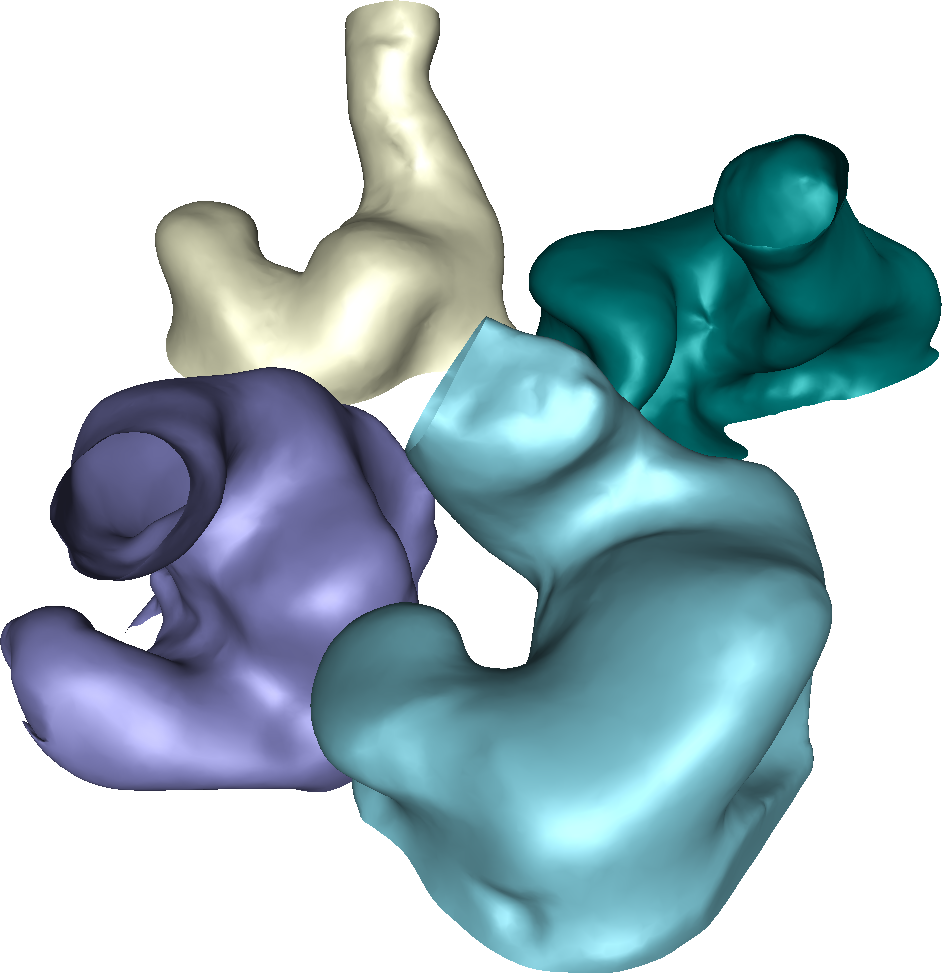
Imagine that you have acquired a set of 3D shapes
using a medical imaging modality and you would like to use some of
the more advanced manifold learning techniques to extract subtle
anatomical information from your set of shapes. This talk introduces
some of the common methods for transforming sets of shapes into a
manifold representation. The talk will focus on shape representation, correspondence, rigid alignment, ICP, non-rigid registration, and Procrustes analysis. Additional Material: R. R. Paulsen, R. Larsen, S. Laugesen, C. Nielsen, B. K. Ersbøll, Building and Testing a Statistical Shape Model of the Human Ear Canal, Medical Image Computing and Computer-Assisted Intervention - MICCAI 2002, 5th Int. Conference, Tokyo, Japan, Springer, 2002 Presentation |
|
| Principal component analysis and independent component analysis | ||
|---|---|---|
| Ole Winther | ||
|
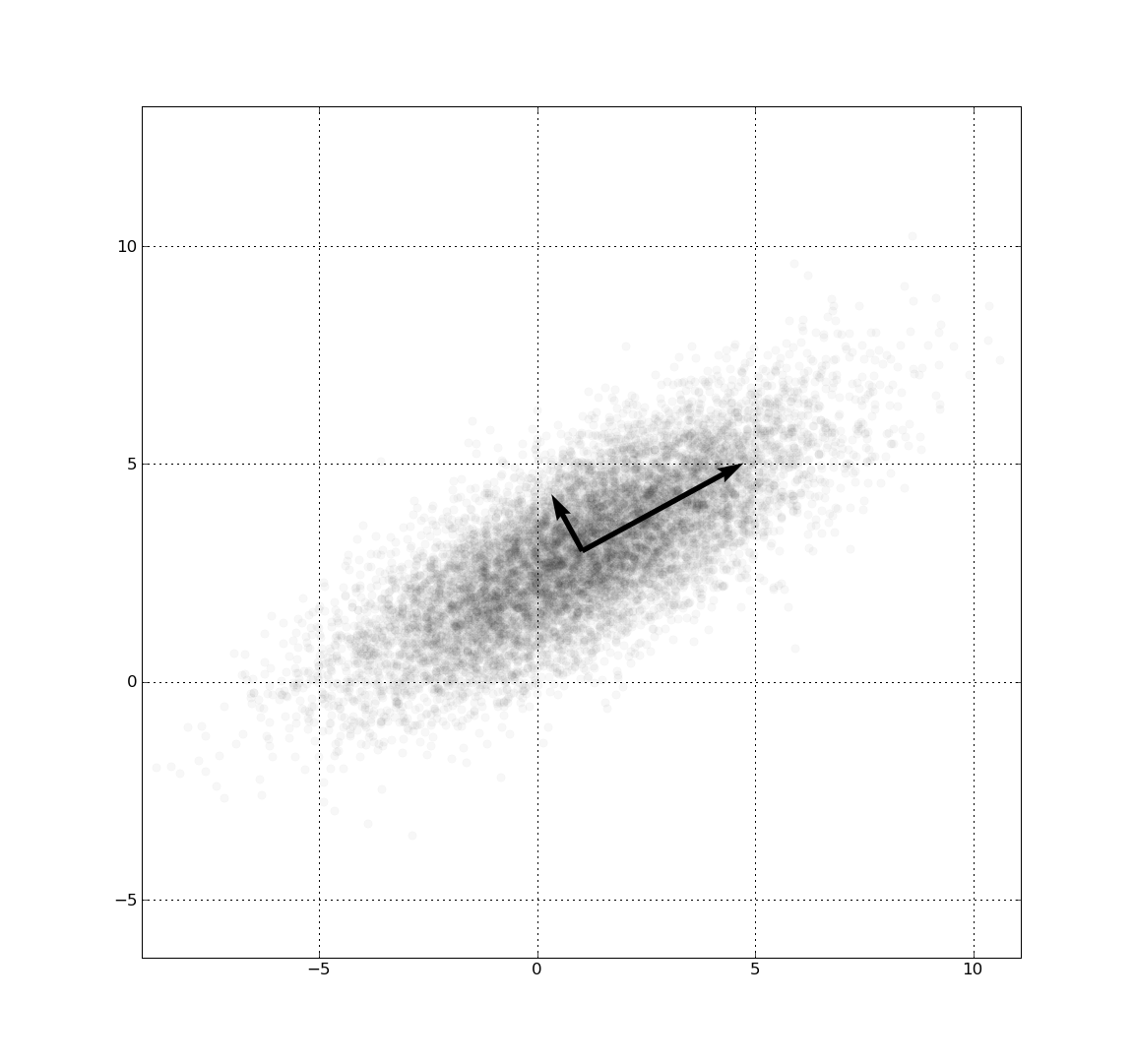
This talk will be journey through linear latent variables models starting from principal component analysis (PCA), continuing through the probabilistic generative model-based approach and finally arriving at the Bayesian solution.
Keywords: PCA, singular value decompostion (SVD), probabilistic PCA (pPCA), identifiabillity, Independent component analysis (ICA), Bayesian approach, sparsity. Presentation |
|
| Manifold learning | ||
|---|---|---|
| Mikhail Belkin | ||
|
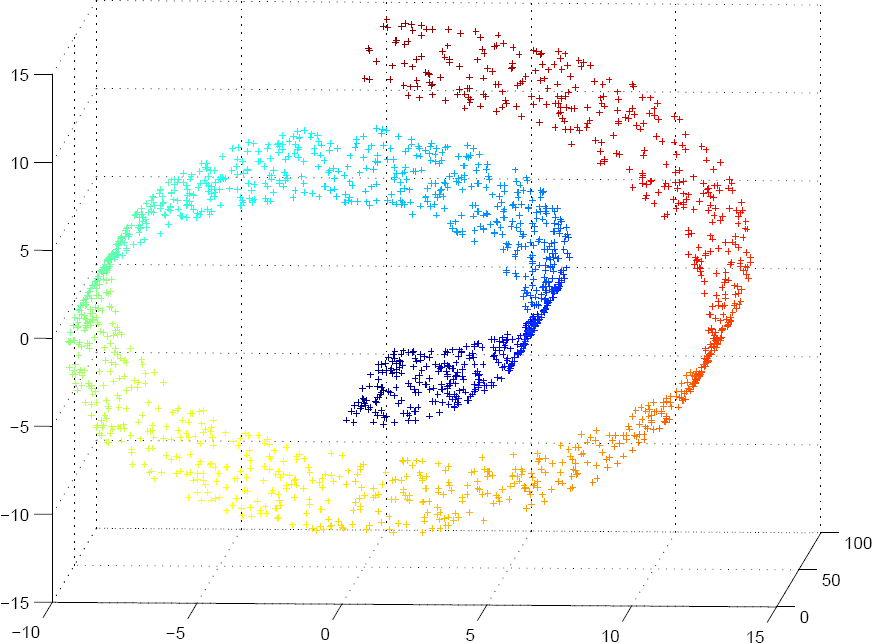
In my tutorial I will introduce the basics of manifold learning
and its connection to graph-based semi-supervised learning. We will
discuss the basics of manifolds and the goals and the applicability
of manifold approaches and some of the applications. In particular,
we will talk about the Laplace operator on the manifold and how the
geometry of data influences the classification boundaries and how
unlabeled data can be useful for classification.
Additional Material: S. Roweis, L. Saul. Nonlinear Dimensionality Reduction by Locally Linear Embedding. JB Tenenbaum, V Silva, JC Langford. A Global Geometric Gramework for Nonlinear Dimensionality Reduction M. Belkin P. Niyogi. Laplacian Eigenmaps for Dimensionality Reduction and Data Representation M. Belkin P. Niyogi. Semi-supervised Learning on Riemannian Manifolds Presentation |
|
| Manifolds and Riemannian geometry | ||
|---|---|---|
| Francois Lauze | ||
| Presentation | ||
| Statistics on manifolds | ||
|---|---|---|
| Thomas Fletcher | ||
|
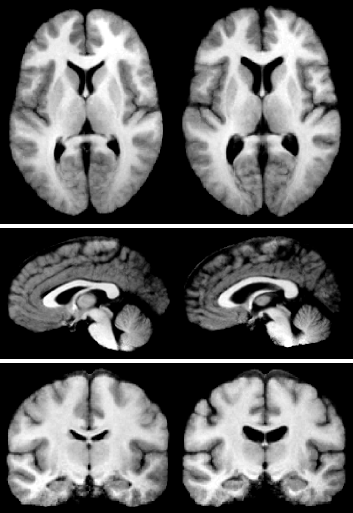
Manifold representations are useful for many different types of data, including directional data, transformation matrices, tensors, and shape.
Statistical analysis of these data is an important problem in a wide range of image analysis and computer vision applications. However, defining statistics on a manifold is not a straightforward process. Even the simplest statistics, such as the mean, depend on the vector space structure of Euclidean space. This structure is not available for a general manifold. In this lecture I will discuss how many common statistics can be defined for manifold-valued data by utilizing the geodesic distance on the manifold. The first example is the mean value of data on a manifold, which can be defined as the point that minimizes the sum-of-squared geodesic distances to the data. Following this example, we can also define variance, principal components analysis, regression, and the median. Computation of all of these statistics is achieved using only two tools, the Riemannian exponential and log mappings. After explaining the algorithms for computing statistics on manifolds, I will demonstrate their application in several image analysis problems.
Additional Material: P.T. Fletcher, S. Joshi, C. Lu, S.M. Pizer. Principal Geodesic Analysis for the Study of Nonlinear Statistics of Shape, IEEE Transactions on Medical Imaging, vol. 23, no. 8, pp. 995-1005, 2004. B. Davis, P.T. Fletcher, E. Bullitt, S. Joshi. Population shape regression from random design data, IEEE International Conference on Computer Vision (ICCV), October, 2007. P.T. Fletcher, S. Venkatasubramanian, S. Joshi. The Geometric Median on Riemannian Manifolds with Application to Robust Atlas Estimation, In Neuroimage, vol. 45, pp. S143-52, 2009. Presentation |
|
| Scientific visualization with manifolds | ||
|---|---|---|
| Lars Kai Hansen | ||
|
Unsupervised learning, independent components, kernel methods, and
the pre-image problem. Neuroimaging, social networks, and audio
signalprocessing.
Presentation |
||
| The meaning of curvature - A distance geometric approach | ||
|---|---|---|
| Steen Markvorsen | ||
|
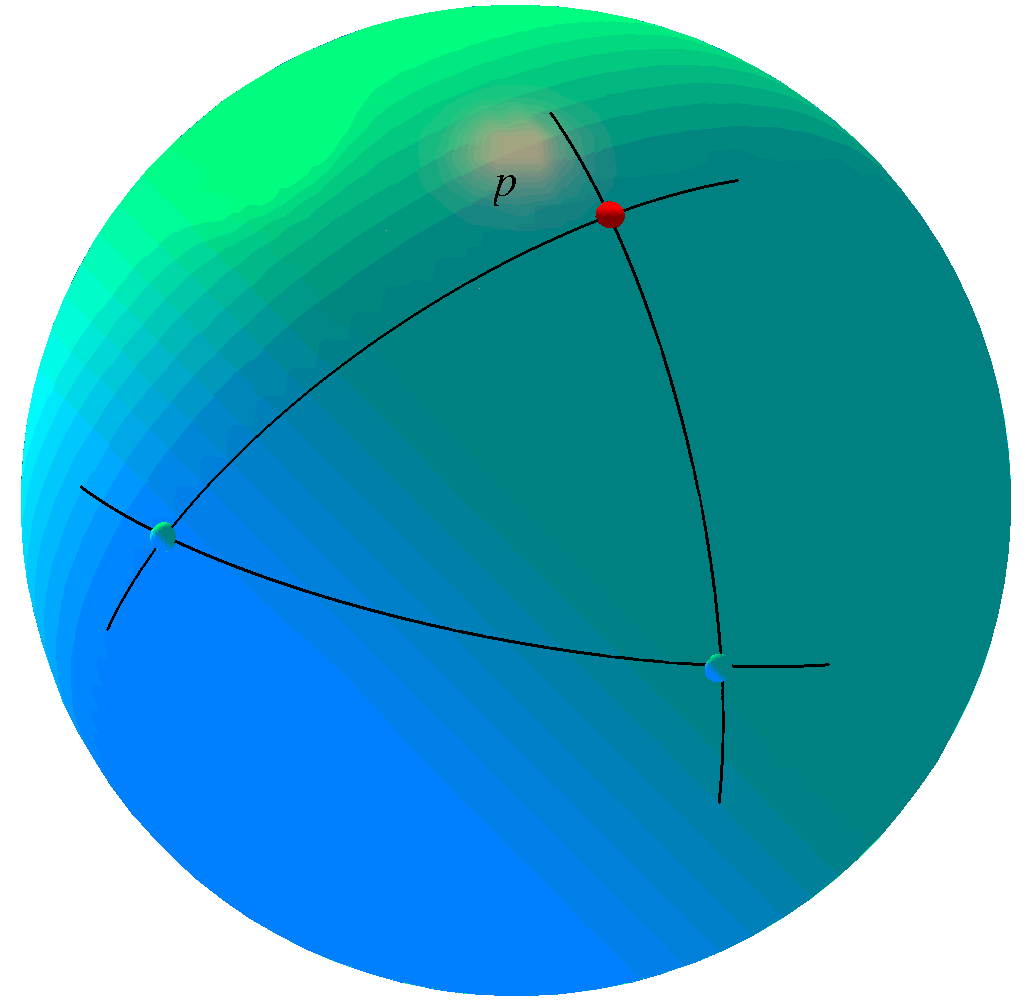
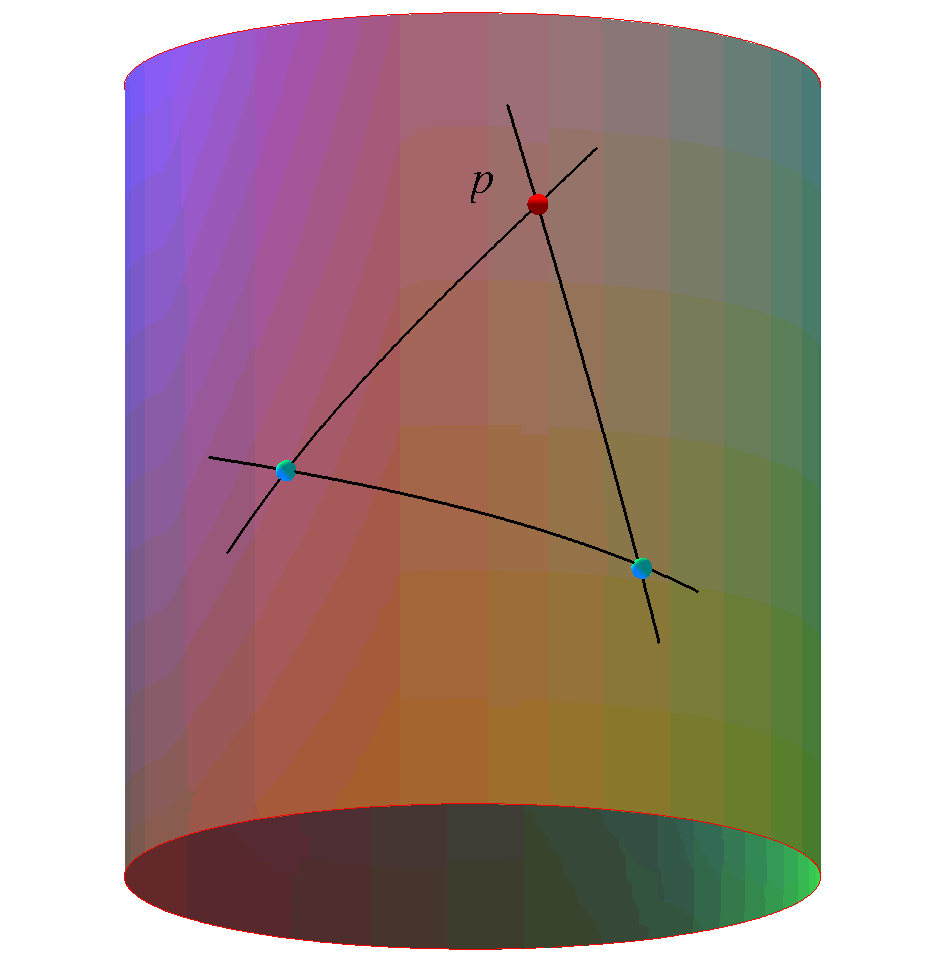
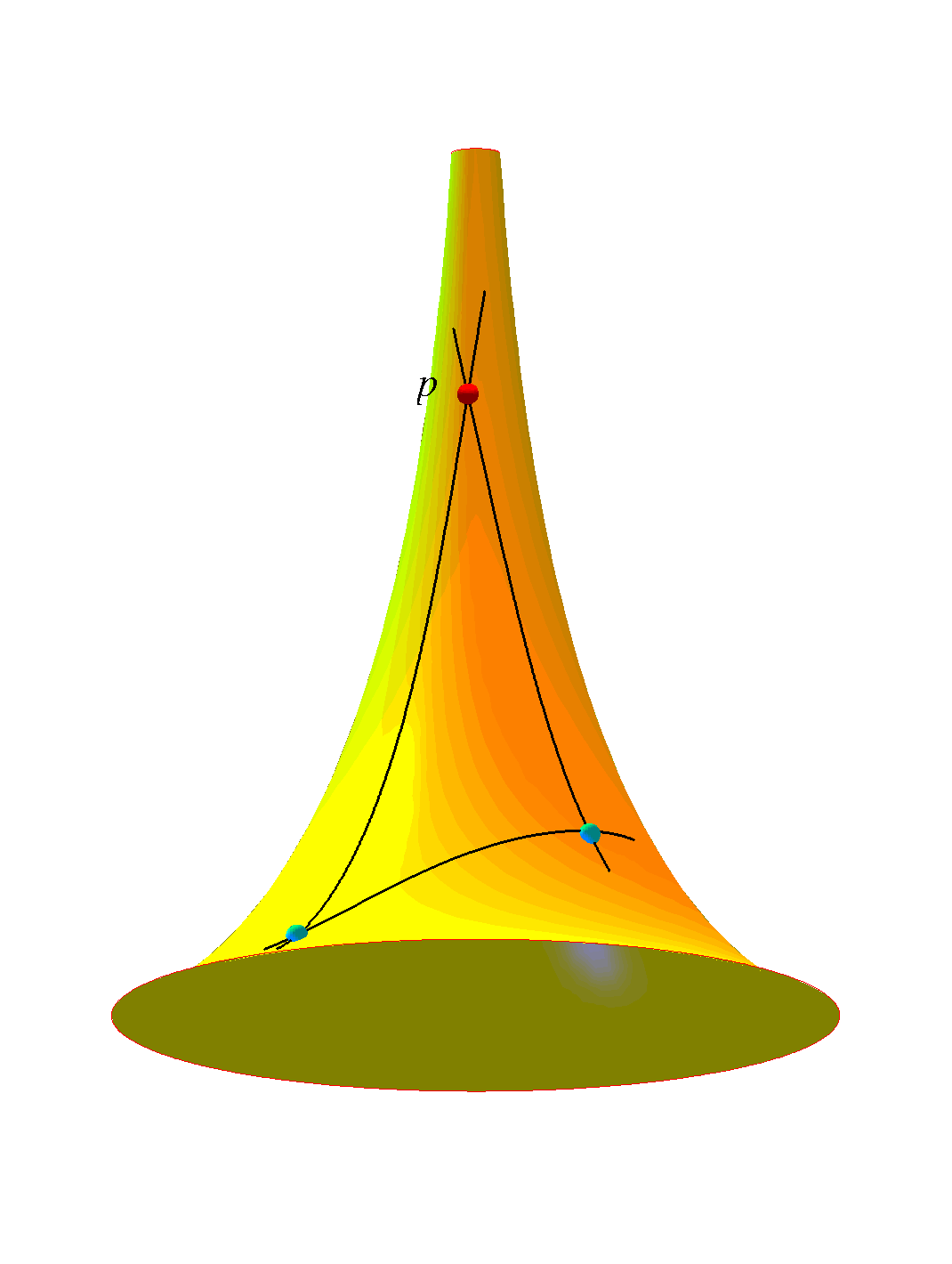
This talk is essentially concerned with the shape
molding forces of curvature and with the old question of how to
detect the presence of curvature in manifolds and length spaces at
various scales ranging from global to local to microlocal. As the old saying goes: Positive curvatures produce fat (geodesic) triangles and negative curvatures slim triangles. Some basic ideas from metric (length-)space geometry and from the geometric analysis of the Laplacian will be surveyed and applied. Via the Laplacian the curvature tensor is in control of a variety of very natural phenomena ranging from heat diffusion to volume growth. We are e.g. interested in obtaining precise bounds for mean exit times for Brownian motions and for isoperimetric inequalities. One way to obtain such bounds are via curvature controlled comparison with corresponding values in constant curvature spaces and in other tailor-made so-called warped product spaces. Additional Material: Ana Hurtado, S. Markvorsen, and Vicente Palmer. Torsional Rigidity of Submanifolds with controlled Geometry. Mathematische Annalen 344 (2009) 511 - 542. S. Markvorsen and V. Palmer. Extrinsic Isoperimetric Analysis on Submanifolds with Curvatures bounded from below. Accepted for publication in Journal of Geometric Analysis (2009). S.Markvorsen. Minimal Webs in Riemannian Manifolds. Geometriae Dedicata 133 (2008) 7 - 34 Presentation |
|
| Sparse statistical models for relating anatomical differences to clinical outcome | ||
|---|---|---|
| Rasmus Larsen | ||
|
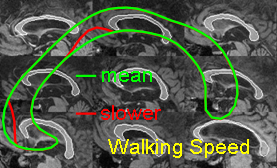
Recent advances in statistics have spawned powerful
methods for regression and data decomposition that promote
sparsity, a property that facilitates interpretation of the results.
Sparse models use a small subset of the available variables and
may perform as well or better than their full counterparts if
constructed carefully. Additional Material: Karl Sjöstrand et al. Sparse Decomposition and Modeling of Anatomical Shape Variation. IEEE Transactions on Medical Imaging. vol: 26, issue: 12, pages: 1625-1635, 2007 H. Zou and T. Hastie. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67(2):301-320, 2005. Presentation |
|
| Human Motion Analysis and Manifolds | ||
|---|---|---|
| Kim Steenstrup Pedersen | ||
|
I will in this lecture give an overview of human motion analysis and how manifold representations naturally arise as representations of the constrained articulated motion performed by humans.
Additional Material: R. Poppe. Vision-based human motion analysis: An overview. Computer Vision and Image Understanding, 108 (1-2): 4-18, 2007. Presentation |
|
| Estimating covariance matrices | ||
|---|---|---|
| Jon Sporring | ||
|
Presentation |
||
| Applications of shape manifolds in medical image analysis. | ||
|---|---|---|
| Mads Nielsen | ||
|
Presentation |
||
Last update September 1, 2009