What is a sparse representation?
Any given data set can be described by a large number of features; mathematically we can describe these features as an overcomplete set of basis vectors for the space in which our data are sitting. More precisely, an observation (say, a signal s) can be written as a linear combination
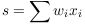
where the x_i are basis vectors. We call the decomposition bove a representation of the signal s. A set of observations with representations (i.e.~a dataset) can be described by a matrix M with entries given by the weights w_i corresponding to each observation or signal. We say that a representation is sparse when many of the w_i are zero, and the sparsity of the representation is reflected by the number of zero elements in M.
What can we get out of this?
First, sparse representations are computationally cheap in data modeling -- the elimination of basis elements efficiently lowers the cost of computation.
Secondly, from the statistical point of view, sparse representations have the advantage of pointing out the important information in your data, and enable you to identify and ignore redundant basis elements. This is, for instance, important in connection with feature selection, where you are able to describe your data exactly with a reduced subset of your original features, as opposed to other dimension reduction methods such as PCA, where elimination of features reduces the exactness of the representation and gives your principal components as linear combinations of your original features. Moreover, as with PCA, the weighting of the different basis elements gives information about how much each basis element is contributing to the properties of your signal.
Thirdly, in practice, models with few non-zero parameters tend to be very stable. Moreover, sparsity regularization can be used to turn ill-posed problems to well-posed, due to the reduced number of parameters.
How?
Geometrically, the problem of finding a sparse representation is formulated in terms of minimizing a cost function which punishes the number of basis elements in the presentation. From the Bayesian point of view, the likelihood function is supplied with a prior (like total variation, pseudo norm, etc.) that favours sparse solutions.
Where is sparsity used?
Applications of sparsity in image and signal analysis include a wide range of topics and techniques, such as image reconstruction, image segmentation, super-resolution, compression, linear regression, feature extraction, graphical model learning, sparse PCA, compressive sensing.