Registration
Registration denotes the proces of aligning geometric objects, e.g. images, points, lines, surfaces, and signals. The summer school on registration aims to enable the participants to work with registration in computer graphics, image and signal analysis, and be able to
- understand 2D and 3D image registration in the above areas,
- understand numerical schemes for representation and optimization in image registration,
- use several similarity measures for image co-registrration,
- use several linear and non-rigid image transformations for image co-registration,
- use relevant optimization schemes for image co-registration,
- use image registration in their research and choose relevant image registration methods to solve their problem,
- have and overview of the use of image registration methods within medical image analysis.
The general setup in registration covers many different types of geometric object but, in order to be concrete, we describe the particular case of image registration below.
Image Registration:
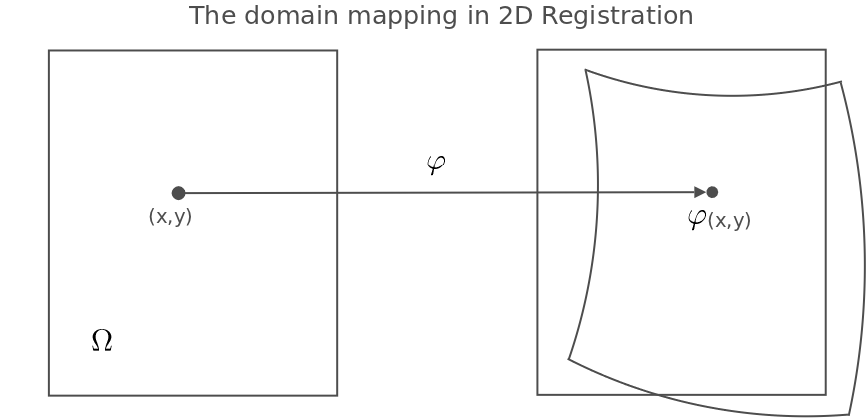
In image registration, a moving image Im is transformed in order to match a fixed image If. If the domain of both images Im and If is denoted Ω, the registration finds a suitable map φ:Ω → Ω so that Im⚪φ is close to If. Registration requires a deformation model to describe and represent the map φ and a similarity measure to measure the closeness between the transformed moving image Im⚪φ and If. In addition, the registration problem is most often ill-posed in the sense that multiple φ exist that can bring Im suitably close to If, and a choice between these candidate φ's must be made. This is performed by a regularization scheme.
Applications:
Image registration plays a fundamental role in a range of applications. Examples include alignment of medical images and image based morphometry, alignment of satellite images in geographical information systems, and alignment of astronomical images.
Variational Formulation:
The combination of regularization and similarity often leads to the registration problem
being formulated as an energy minimizing tasks: If we let R(φ) denote the reqularization measure,
let S(Im⚪φ,If) be the similarity measure, and let λ be a weight,
the optimal φ can be found by minimizing
E(φ) = R(φ) + λS(Im⚪φ,If) .
Degrees of Freedom:
There exists different choices for the allowed range of deformations φ. Most often an affine or rigid registration is used to remove the effect of rotation, translation, and, in the affine case, scaling. A closer match can then be obtained by extending the set of admissble φ and hence allowing more freedom in the transformation. These non-rigid transformations have more degrees of freedom, from many to infinite, and the require in particular a computational representation.
Deformation Models and Computational Representations:
Various ways of representing φ exist, each with pros and cons in terms of smoothing properties, computational complexity, and numerical stability. Among the most widely used are B-spline basis functions that interpolates between a finite number of control points distributed over the image domain Ω. The smoothness of B-splines and the finite number of control points provide implicit regularization, and B-splines are computationally practical.
A more mathically oriented deformation model is the large deformation diffeomorphic metric mapping framework (LDDMM) that models φ as the solution of a differential equation. This provides the registration setup with a Riemannian manifold structure and a solid mathematical foundation.
A range of other methods are in use, to many to be listed here: various flavours of the Demons algorithm, fluid registration methods, etc.
Image Similarities:
Perhaps the simplest and most widely used measure for similarity between images is the
sum of squared errors:
S(Im⚪φ,If)
=
ΣΩ|Im⚪φ(x)-If(x)|2dx .
SSE can be problematic in several ways, for example if the images are illuminated differently.
Statistical measures such as cross correlation, mutual information, and normalized mutual information
seek to avoid some of the deficiencies of SSE.

