OceanWave3D / MarineSEM - Fully Nonlinear and Dispersive free surface wave modelling


|
|


| |

| |

 | |

|
 |
 | |
 |
 |
Mission
Research, improve and develop robust, fast and accurate methodologies for large-scale fully nonlinear and dispersive free surface modelling, highly accurate kinematics in the entire fluid domain and nonlinear wave-structure and moving wave-body methods for marine offshore engineering applications.
Contributors
| Software | Responsible lead developer | Key reference |
| OceanWave3D-FDM (Fortran 90) | Allan P. Engsig-Karup (DTU) | Engsig-Karup, Lindberg & Bingham (2008) |
| OceanWave3D-GPU (C/C++) | Allan P. Engsig-Karup (DTU) | Engsig-Karup, Madsen & Glimberg (2011) |
| GPULAB Library + OceanWave3D-GPU (C/C++) | Stefan Lemvig Glimberg / Allan P. Engsig-Karup (DTU) | Glimberg (2013) |
| OceanWave3D-NSE | Allan P. Engsig-Karup | Allan Peter Engsig-Karup & Anders Melander (2024) |
| MarineSEM | Allan P. Engsig-Karup (DTU) / Claes Eskilsson (RISE) | Engsig-Karup, Eskilsson & Bigoni (2016) |
| Nektar++ FNPF | Andreas Mieritz (DTU) / Allan P. Engsig-Karup (DTU) | - |
| Module | Responsible lead developer | Key reference |
| Algorithms, Iterative solvers, Performance & Applications | Allan P. Engsig-Karup (DTU) | Engsig-Karup et al. (2008), Engsig-Karup (2014), Engsig-Karup & Laskowski (2020) |
| SWENSE method | Guillaume Ducrozet (LHEA) / Allan P. Engsig-Karup (DTU) | Ducrozet, Engsig-Karup, Bingham & Ferrant (2013) |
| Immersed Boundary (IB) method | Ole Lindberg (DTU/FORCE) & Stavros Kontos (DTU) | Kontos (2016) |
| Waves2Foam | Bo Terp Paulsen (DTU) | Paulsen, Bredmose & Bingham (2014) |
| Irregular waves / Multidirectional waves | Harry Bingham (DTU) | - |
| Wave breaking | Harry Bingham (DTU) | - |
| Uncertainty Quantification | Daniele Bigoni (DTU) / Allan P. Engsig-Karup (DTU) | Bigoni, Engsig-Karup, Eskilsson (2015) |
| Fixed, Forced and Free Wave-body applications | Allan P-. Engsig-Karup (DTU) | Engsig-Karup, Monteserin & Eskilsson (2017,2018), Visbech, Engsig-Karup & Bingham (2022) |
| Free surface Navier-Stokes / CFD | Allan Peter Engsig-Karup (DTU) | Engsig-Karup & Melander (2024) |
OceanWave3D newsletter
Sign up to the OceanWave3D newsletter to get the latest information about open source OceanWave3D. Sign up here: LINK.
Background
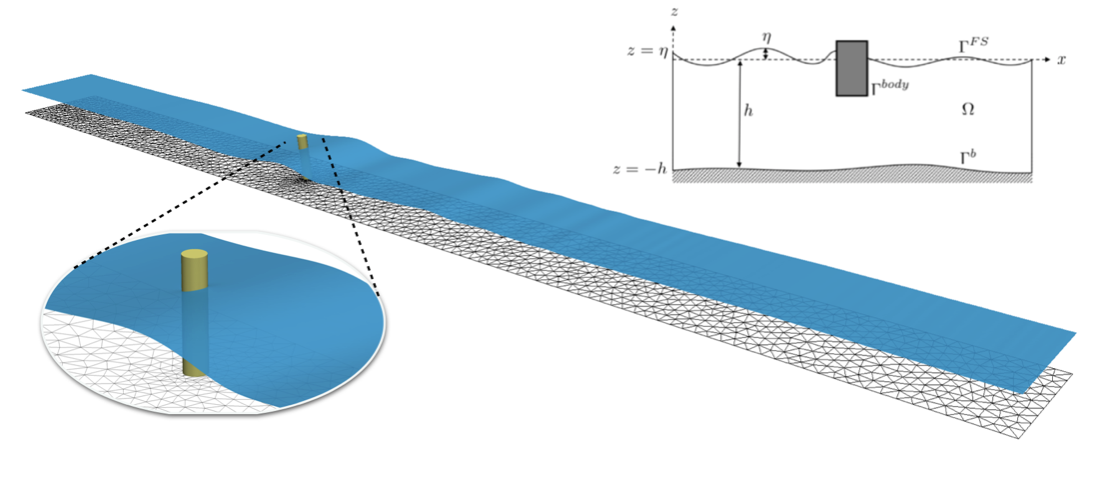
For efficient simulation of free surface flow over variable depth in coastal and offshore engineering a first Boussinesq model was derived by Peregrine (1976). This model was restricted to accurate simulations in shallow waters. The equations were later extended for the adaption to deeper waters. This led to the development of several modified forms of Boussinesq-type equations, e.g. Madsen et al. (1992) and Nwogu (1993) and later Madsen et al. (2003). Motivated by some of these original and successfull developments Engsig-Karup et al. (2008) developed a robust and efficient flexible-order finite difference model based on a fully nonlinear and dispersive potential flow model which was thereafter referred to The OceanWave3D model. The OceanWave3D model seek to address the limitations in practical application ranges of most Boussinesq-type models stemming from the inherent analytical approximations, and is in addition inspired by the original work by Li and Fleming (1997) who were the first to propose a low-order multigrid method for efficient and scalable solution of the fully nonlinear potential flow equations for water wave applications. Extensions to the work of Li and Fleming (1997) focusing on improved efficiency via high-order discretizations have been analyzed and demonstrated by Bingham et al. (2007), however, this high-order extension had similar robustness issues as discussed in Li and Fleming (1997). Further improvements in both efficiency and robustness is described in Engsig-Karup et al. (2008) for a complete model in three space dimensions. These developments suggested that the original algorithmic strategy due to Li and Fleming could be generalized to a flexible-order finite difference discretization in three space dimensions and then mapped with high efficiency to Graphics Processing Units (GPUs) by Engsig-Karup, Madsen and Glimberg (2011) to significantly leverage the performance of the fully nonlinear potential flow model. This work was initially aimed at closing the performance gap between traditional Boussinesq-type models and volumen-based solvers such as the fully nonlinear potential flow (FNPF) model and enabled for the first time fast (near) real-time nonlinear hydrodynamics calculations at unpreceedented speed for such a model, cf. Engsig-Karup, Madsen and Glimberg (2011) on the feasibility of real-time computations. The model was developed to enable efficient massively parallel computations for arbitrary sized (large-scale) problems on modern heterogeneous many-core hardware and analyzed with benchmarks in more detail by Engsig-Karup (2014) confirming robustness and efficiency of the model. Several novel improvements of the above-mentioned developments of the work are described in Ducrozet et al. (2012), Ducrozet et al. (2013), Engsig-Karup et al. (2014), Paulsen et al. (2014), Bigoni et al. (2015) and Engsig-Karup et al. (2016) and Duz et al (2016). In particular, the work of Engsig-Karup et al. (2016) represents new progress since Robertson & Sherwin (1999) for the development of a robust multi-domain methodology using the Spectral Element Method for simulation of highly nonlinear and dispersive wave propagation giving opportunity for accurate wave propagation and kinematics together with use of flexible (possibly adapted) unstructured meshes for nonlinear wave-structure interactions applications as described in Engsig-Karup et al. (2017) and for nonlinear wave-body interactions in Monteserin et al. (2018) aimed at realistic marine settings and engineering purposes.
The OceanWave3D model can be viewed as merely a 'discrete free surface model' of the Fully Nonlinear and Dispersive Potential Flow equations with application range limited only by the truncation errors introduced in the discretization procedure and the assumptions behind the model, namely, that it is potential flow. However, the application range for the fully nonlinear and dispersive potential flow model are quite broad and is a key enabler for many practical applications. The novel parallel numerical algorithms and efficient implementations combined with the use of modern technology makes it possible to achieve high performance making it feasible as a base solver for novel engineering analysis and engineering applications. To advocate reproducible science and contribute to stimulate fundamental research and strategic collaborations aimed at delivering more advanced engineering tools, the software is delivered as open source (see licensing terms and copyright terms below). We encourage the growing community of users to contribute back the experiences and developments, to continue advancing the technology base.
Research
The open source OceanWave3D model has been developed at Technical University of Denmark since 2006 as a part of ongoing research efforts with Assoc. Prof. Allan P. Engsig-Karup. All main parts of released software with state-of-the-art algorithms and implementations have been developed and implemented at Department of Applied Mathematics and Computer Science (DTU Compute) since 2008.
The research activities at DTU Compute focus on development, benchmarking and application of new algorithms and new analysis techniques for the development of robust and fast numerical tools and enabling proper use of modern technology for scientific calculations directed towards advanced engineering applications.
Model features
The OceanWave medthodology developed at Department of Applied Mathematics and Computer Science (DTU Compute) has been designed to enable fast(!) and robust engineering analysis of wave propagation in marine areas.
Some key Oceanwave3D model features are given below.
The model has been designed and implemented to enable
- General-purpose, robust and highly efficient computations with documented efficiency.
- Flexible-order finite difference discretization enabling both h- and p-refinement strategies for optimally balancing accuracy and work. This also means that both low-order and high-order accuracy in the discretization is available (most other models have only low order accuray available hindering accurate long time simulations).
- Flexible with respect to geometry via adaptive and curvilinear meshes.
- Efficient and scalable Multigrid Preconditioned Defect Correction (PDC) Method for iterative solution of Laplace problem for flexible-order discretizations.
- Explicit and robust time-integration using a stage-optimized fourth-order Runge-Kutta method. A unique property is the model has conditional CFL stability which is governed only by the physics resolved and not by the numerics (which is usually the case for high-order discretizations and refined grids).
- Large-scale simulations through data-parallel MPI-based domain decomposition method. The multi-GPU version of the OceanWave3D model can solve problems of arbitrary many degrees of freedom on the largest modern super computing clusters in the world with ideal scaling. Currently, tests have been done with excellent weak scalability (fx. Oakridge GPU cluster with up to 8.192 GPUs). For example, problems up to about 10.000.000.000 degrees of freedom in the volumetric mesh can be simulated using 64 multi-device CPU-GPUs.
- Fast analysis via a Massively parallel MPI-CUDA multi-GPU multiblock implementation on heterogeneous and modern many-core hardware.
- Affordable and efficient computations using commodity hardware. For example, a single GPU version of the OceanWave3D model can solve problems with close to 150.000.000 degrees of freedom in the volumetric mesh for the laplace problem in single precision and using 6GB RAM and process one iteration of the efficient iterative solver in less than 1 second on a Fermi GPU.
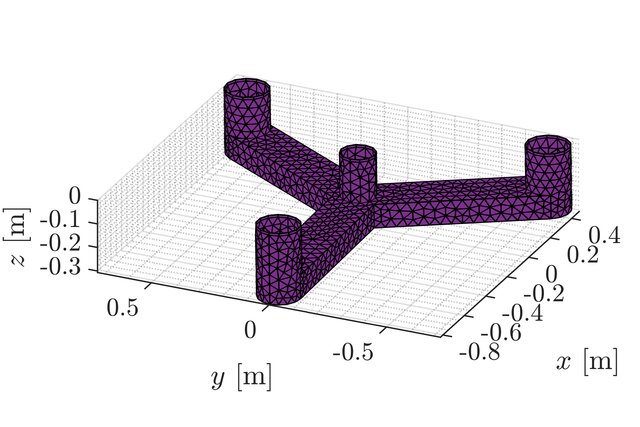
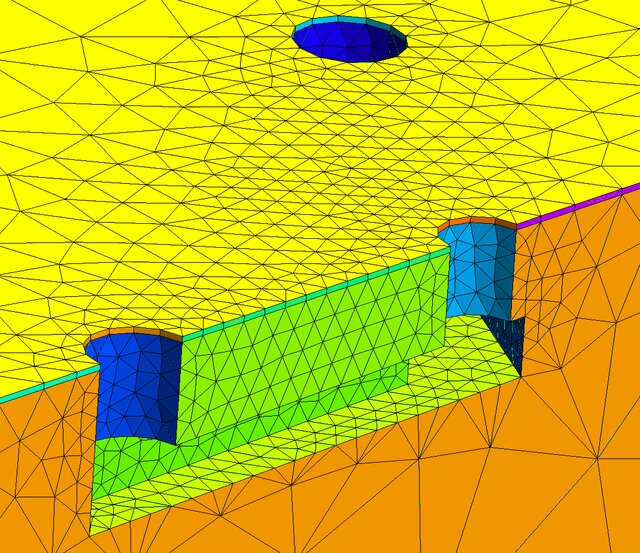
- Adaptive unstructured spectral element model with high mesh flexiblility to model coastal and marine areas.
- Nonlinear wave-structure and wave-body interactions enabled in the spectral element model for arbtirarily shaped fixed, surface-piercing and floating bodies.
Source code
The OceanWave3D software exist in several versions (Fortran 90 and C++) and currently the Fortran 90 version has been prepared to be used freely under the terms of the GNU Lesser General Public License v3. For any use of the OceanWave3D source code in your environment and reporting proper reference must be made to the origin of the software.
Please cite the following reference(s) to support the work.
The OceanWave3D or OceanWave3D-CPU version is first presented in
@ARTICLE{EngsigKarupEtAl08,
AUTHOR = "Engsig-Karup, A.P. and Bingham, H.B. and Lindberg, O.",
TITLE = "An efficient flexible-order model for {3D} nonlinear
water waves",
YEAR = "2009",
JOURNAL = "Journal of Computational Physics",
VOLUME = "228",
PAGES = "2100-2118"
}
DOWNLOAD from GITHUB: OceanWave3D-Fortran90.
Remark, there is now an EASY INSTALLATION option that is currently experimental that is done via Docker, cf. the 'botp' branch in the above github repository.
The GPU-accelerated version OceanWave3D-GPU is first presented in
@article {EngsigKarupEtAl2011,
author = {Engsig-Karup, A. P. and Madsen, Morten G. and Glimberg,
Stefan L.},
title = {A massively parallel GPU-accelerated model for analysis of
fully nonlinear free surface waves},
journal = {International Journal for Numerical Methods in Fluids},
volume = {70},
number = {1},
publisher = {John Wiley & Sons, Ltd},
year = {2012},
}
A unique massively parallel and massively scalable implementation has
been done in the GPULAB Library which
is presented in
@INPROCEEDINGS{GlimbergEtAl13,
AUTHOR = "Glimberg, L. S. and Engsig-Karup, A. P. and Nielsen,
A. S. and Dammann, B.",
TITLE = "Development of software components for heterogeneous
many-core architectures",
EDITOR = "Raphael Couturier",
BOOKTITLE = "Designing Scientific Applications on GPUs",
SERIES = "Lecture notes in computational science and engineering",
PAGES = "73--104",
PUBLISHER = "CRC Press / Taylor \& Francis Group",
YEAR = "2013"
}
We have a version of the

GPULAB library by
DTU Compute that is available with a
license defined by the
Creative Commons
Attribution 4.0 International License.
Request for direct access to the software can happen by E-mail apek @ dtu . dk with a statement of intended purpose of application. It is possible to contribute to the project.
Applications
The general-purpose fully nonlinear potential flow (FNPF) model is used in several academic/industrial applications, e.g. for
- Real-time interactive ship-wave hydrodynamics in an industrial full mission simulator. See Project description.
- Hybrid model for wave-structure interactions possible through a multi-physics hybrid coupling of OceanWave3D and Euler-viscous solver. Learn more from the proof-of-concept report: LINK>
- Hybrid models for wave-structure interactions possible through a multi-physics hybrid couplings
- Wave-structure interaction using a multi-model method for simulating 2D Surface-Piercing Wave-Structure Interactions based on coupling OceanWave3D and an OpenFoam RANS solver. Learn more from Ph.D. thesis: LINK.
- OceanWave3D and Smooth Particle Hydrodynamics (SPH) model. Learn more from the proof-of-concept paper: LINK
- Violent wave-structure interactions possible through multi-physics hybrid 1-way coupling of OceanWave3D and Refresco (Urans/VOF). Learn more from comparison paper: LINK.
- Violent wave-structure interactions enabled through a multi-physics hybrid 2-way coupling of OceanWave3D and SPHysics. See LINK.
- Violent wave-structure interactions enabled through a multi-physics hybrid 1-way coupling of OceanWave3D and OpenFOAM (VOF). See the waves2Foam package description along with this release information Release Oct. 15, 2015. with announcement Public release.
- Efficient and accurate numerical wave tank experiments. Wave load project results.
- Large-scale simulation of coastal areas where the sea floor varies. This makes it possible to predict local wave climates for coastal regions.
- Very accurate prediction of kinematics from sea floor to free surface which may be used in wave- or flow-induced structural loads. See Numerical experiments.
- Development of new tools for added resistance and maneurering calculations of ships at slow forward speed in european SHOPERA consortium. See Project announcement.
- Prediction of fully nonlinear wave-structure interactions in marine areas or regions and take into account real geometry of fixed and moving structures.
- Stochastic wave simulations for uncertainty quantification.
- DTU Compute GPULAB library and the OceanWave3D-GPU module is used in the large Danish joint Academic-Industry project DeRisk (2015-2019).
- Independent Benchmarking study of OceanWave3D can be found in M.Sc. thesis project titled "Non-linear Irregular Wave Impact on Monopile Structures" due to Philipp Schopfer (2016), NTNU. Another independent study can be found here PhD thesis due to Maite Gouin (2016), Ecole Centrale Nantes.
- Fully nonlinear Wave-body simulations for offshore engineering and renewable wave energy sector applications.
- Participation in A Collaborative Computational Project in Wave Structure Interaction (CCP-WSI) with a MarineSEM solver. Learn more from the paper with results from the blindtest experiment presented at ISOPE 2018 (Pre-conference) and ISOPE 2019 (Post-conference).
- Proof-of-concept using FNPF-SEM on a heaving decay test for a free body generating nonlinear wave motions, see Heaving Decay Test.
- Efficient and scalable simulations using p-multigrid Spectral Element methods, cf. Engsig-Karup & Laskowski (2020).
- A FNPF-SEM solver from MarineSEM was used as a higher fidelity model in Multi-fIdelity Decision making tools for Wave Energy SysTems (MIDWEST) funded via the EU-OceaneraNET program by the French ADEME, by the Swedish SWEA, and by the Portuguese FCT.
Ongoing research seek to address or explore new types or aspects of next-generation modeling and applications.
If you have an application or a project described online somewhere where the OceanWave3D / MarineSEM solvers are used (or could be used), E-mail apek @ dtu . dk and give directions to proper referencing to get it listed here.
Recent talks
- A. P. Engsig-Karup, Very fast simulation of nonliner water waves in very large numerical wave tanks on affordable graphics cards, Workshop on GPU computing today and tomorrow
- A.P. Engsig-Karup, SDU Days of Scientific Computing, Southern Danish University, 2012. Program
- A. P. Engsig-Karup, Massively Parallel Computational Hydrodynamics for Sustainable Energy Source Applications, HPC Core Workshop, United Kingdom, April, 2016.
- A. P. Engsig-Karup, On recent progres on the development of new general-purpose fully nonlinear marine hydrodynamics models for wave propagation and wave-body applications, Hydrodynamics of Wave Energy Converters (HYWEC), Bilbao, Spain, April, 2017.
- A. P. Engsig-Karup, Spectral Element Methods for Nonlinear Wave-Structure Interactions in Marine Hydrodynamics, Nektar++ Workshop 2017, London, United Kingdom, June, 2017
- C. Eskilsson and A.P. Engsig-Karup, Spectral Element Methods for Wave and Wave-Body Modelling, DNV GL WORKSHOP, DTU, Denmark, January, 2018.
- A.P. Engsig-Karup, DANSIS seminar day on High order discretisation methods in CFD, Aarhus, Denmark, March, 2018. Presentation slides available.
- A.P. Engsig-Karup, High-order Accurate Fully Nonlinear Potential Flow Time-Domain Methods for Marine Hydrodynamics, 1st International Workshop on Marine Hydrodynamics Modelling, Harbin, China, May 21-25, 2018.
- A.P. Engsig-Karup and C. Eskilsson, Spectral Element FNPF Simulation of Focused Wave Groups Impacting a Fixed FPSO. ISOPE 2018, Japan.
- A.P. Engsig-Karup, Advances and challenges in hydrodynamic simulation methods, Wind Energy Denmark, Hedensted, Denmark, October 30, 2018.
- A.P. Engsig-Karup, High-Order Numerical Methods for Nonlinear Wave and Wave-Structure Interaction for Engineering Applications, 2nd International Workshop (online) on Numerical and experimental modelling of wave structure interactions, 17-26 November, 2020.
- A.P. Engsig-Karup, High-Order Numerical Methods for Nonlinear Free Surface Waves and Wave-Structure Interaction for Engineering Applications, MATHICSE Seminar, 19 December, 2023, EPFL, Switzerland.
- A.P. Engsig-Karup and Anders Melander, A High-Order Finite Difference Incompressible Navier-Stokes model for Water Waves and Wave-Structure Interaction, 39th IWWWFB, Scotland, April 17, 2024.
Peer-Reviewed Publications related to advancing the fundamental methods
- Li, B. and Fleming, C. A. A three dimensional multigrid model for fully nonlinear water waves. 1997. Coastal Engineering, Vol 30: 235-258.
- Robertson, I. and Sherwin, S. Free-Surface Flow Simulation Using hp/Spectral Elements. Journal of Computational Physics 155, 26--53 (1999).
- H. B. Bingham and H. Zhang. On the accuracy of finite-difference solutions for nonlinear water waves. J. Engng. Math., 58:211-228, 2007.
- A. P. Engsig-Karup, H. B. Bingham and O. Lindberg. An efficient flexible-order model for 3D nonlinear water waves. December, 2008. Journal of computational physics, 228, pp. 2100--2118.
- Engsig-Karup, A. P., Madsen, M. G. and Glimberg, S. L. 2011 A massively parallel GPU-accelerated model for analysis of fully nonlinear free surface waves. In International Journal of Numerical Methods in Fluids Volume 2012; 70(1):20-36.
- Ducrozet, G., Bingham, H. B., Engsig-Karup, A. P., Bonnefoy, F. and Ferrant, P. 2012 A comparative study of two fast nonlinear free-surface water wave models. In International Journal for Numerical Methods in Fluids 08/2012; 69(11):1818-1834.
- Ducrozet, G., Engsig-Karup, A. P., Bingham, H. B. and Ferrant, P. 2013 A non-linear wave decomposition model for efficient wave-structure interaction. Part A: Formulation, validations and analysis. In Journal of Computational Physics 09/2013; 257:863-883.
- Glimberg, S. L., Engsig-Karup, A. P., Dammann, B. and Nielsen, A. S. 2013. (ISBN: 978-1-4665-7162-4) In book: Designing Scientific Applications on GPUs, Chapter: Development of High-Performance Software Components for Emerging Architectures, Publisher: Taylor & Francis, Editors: Raphael Couturier, pp.73-104.
- Engsig-Karup, A. P., Glimberg, S. L., Nielsen, A. S. and Lindberg, O. 2013. (ISBN: 978-1-4665-7162-4) In book: Designing Scientific Applications on GPUs, Chapter: Fast hydrodynamics on heterogenous many-core hardware, Publisher: Taylor & Francis, Editors: Raphael Couturier, pp.251-294.
- Engsig-Karup, A. P. 2014 Analysis of efficient preconditioned defect correction methods for nonlinear water waves. Accepted for publication in International Journal of Numerical Methods in Fluids.
- Paulsen, B. T., Bredmose, H. and Bingham, H. B. 2014. An efficient domain decomposition strategy for wave loads on surface piercing circular cylinders. In Coastal Engineering, Volume 86, Pages 57-76.
- Bigoni, D., Engsig-Karup, A.P. and Eskilsson, C. A Stochastic Nonlinear Water Wave Model for Efficient Uncertainty Quantification. In http://arxiv.org. 2015.
- Engsig-Karup, A.P., Eskilsson, C. and D. Bioni. A Stabilised Nodal Spectral Element Method for Fully Nonlinear Water Waves. In Journal of Computational Physics, Volume 318, 1 August 2016, Pages 1-21.
- Duz, B., Bunnik, T., Kapsenberg, G. and Vaz, G. Numerical simulation of nonlinear free surface water waves - coupling of a potential flow solver to a URANS/VOF code. OMAE2016, 2016.
- Engsig-Karup, A.P., Eskilsson, C. and Bigoni, D. Unstructured Spectral Element Model for Dispersive and Nonlinear Wave Propagation. ISOPE2016, 2016.
- Engsig-Karup, A.P., Monteserin, C. and Eskilsson, C. A Stabilised Mixed Eulerian Lagrangian Spectral Element Method for Nonlinear Wave Interaction with Fixed Structures. E-published at arXiv.org, 27 March, 2017.
- Glimberg, S.L., Engsig-Karup, A.P. and Olson, L.N. A massively scalable distributed multigrid framework for nonlinear marine hydrodynamics. The International Journal of High Performance Computing Applications, 2019.
- Verbrugghe, T., Devolder, B., Dominguez, J.M., Kortenhaus, A. and Troch, P. Feasibility study of applying SPH in a coupled simulation tool for wave energy converter arrays. 12th European Wave and Tidal Energy Conference (EWTEC), 2017.
- Verbrugghe, T., Kortenhaus, A., Troch, P., and Dominguez, J.M. A non-linear 2-way coupling between DualSPHysics and a wave propagation model, Conference: 12th International SPHERIC Workshop, At Ourense, June 2017.
- Hui Xu, Chris D. Cantwell, Carlos Monteserin, Claes Eskilsson, Allan P. Engsig-Karup, and Spencer J. Sherwin. Spectral/hp element methods: Recent developments, applications, and perspectives, Journal of Hydrodynamics, February 2018, Volume 30, Issue 1, pp. 1-22.
- Engsig-Karup, A.P. and Eskilsson, C. Spectral Element FNPF Simulation of Focused Wave Groups Impacting a Fixed FPSO. ISOPE 2018.
- Koukounas, D., Eskilsson, C. and Engsig-Karup, A.P. Numerical Simulations of Peregrine Breathers using a Spectral Element Model. OMAE 2018.
- Monteserin, C., Engsig-Karup, A.P., and Eskilsson, C. Nonlinear Wave-body Interaction using a Mixed-Eulerian-Lagrangian Spectral Element Model. OMAE 2018.
- Ransley, E., Yan, S. , Brown, S. A., Mai, T., Graham, D., Ma, Q., Musiedlak, P-H., Engsig-Karup, A. P., Eskilsson, C., Li, Q., Wang, J., Xie, Z., Venkatachalam, S., Stoesser, T., Zhuang, Y., Li, Q., Wan, D., Chen, G., Chen, H., Qian, L., Ma, Z., Mingham, C., Causon, D., Gatin, I., Jasak, H., Vukcevic, V., Downie, S., Higuera, P., Buldakov, E., Stagonas, D., Chen, Q., Zang, J. and Greaves, D. (2019). A Blind Comparative Study of Focused Wave Interactions with a Fixed FPSO-like Structure (CCP-WSI Blind Test Series 1). International Journal of Offshore and Polar Engineering, 29(2), pp. 113-127.
- Engsig-Karup, A.P. and Eskilsson, C. Spectral Element FNPF Simulation of Focused Wave Groups Impacting a Fixed FPSO-type Body. International Journal of Offshore and Polar Engineering (IJOPE), March, 2019.
- Engsig-Karup, A.P., Monteserin, C. and Eskilsson, C. A Mixed Eulerian-Lagrangian Spectral Element Method for Nonlinear Wave Interaction with Fixed Structures. Water Waves volume 1, pages 315-342(2019).
- Engsig-Karup, A.P. and Laskowski, W. Efficient p-multigrid spectral element model for water waves and marine offshore structures. Arxiv.org, September, 2020.
- V. Sriram, S. Agarwal, S. Yan, Z. Xie, S. Saincher, T. Schlurmann, Q. Ma, T. Stoesser, Y. Zhuang, B. Han, W. Zhao, X. Yang, Z. Li, D. Wan, Y. Zhang, B. Teng, D. Ning, N. Zhang, X. Zheng, G. Xu, J. Gong, Y. Li, K. Liao, W. Duan, R. Han, W. Asnim, Z. Sulaiman, Z. Zhou, J. Qin, Y. Li, Z. Song, X. Lou, L. Lu, C. Yuan, Y. Ma, C. Ai, G. Dong, H. Sun, Q. Wang, Z.-T. Zhai, Y.-L. Shao, Z. Lin, L. Qian, W. Bai, Z. Ma, P. Higuera, E. Buldakov, D. Stagonas, S. M. Lopez, A. Christou, P. Lin, Y. Li, J. Lu, S. Y. Hong, Y.-J. Ha, K.-H. Kim, S.-K. Cho, D.-M. Park, W. Laskowski, C. Eskilsson, M. Ricchiuto, A.P. Engsig-Karup, L. Cheng, J. Zheng, H. Gu, G. Li. A Comparative Study on the Nonlinear Interaction Between a Focusing Wave and Cylinder Using State-of-the-art Solvers: Part A. International Journal of Offshore and Polar Engineering, Vol. 31, No. 1, March 2021, pp. 1-10.
- Mortensen, L.K., Laskowski, W., Engsig-Karup, A.P., Eskilsson, C. and Montesering, C. Simulation of Nonlinear Waves Interacting with a Heaving Body using a p-Multigrid Spectral Element Method, ISOPE 2021, Rhodos, Grece.
- Visbech, J.H., Engsig-Karup, A.P. and Bingham, H.B. A spectral element solution of the 2D linearized potential flow radiation problem. Int. J. Num. Fluids, 11 October, 2022.
Preprints (submitted for review in journals)
PhD theses (Research on advanced Fully Nonlinear Potential Flow Modelling Tools at DTU)
- Engsig-Karup, A. P. Unstructured Nodal {DG-FEM} solution of high-order Boussinesq-type equations (2006), Department of Mechanical Engineering, Technical University of Denmark.
- Glimberg, S. L. Designing Scientific Software for Heterogeneous Computing - With application to large-scale water wave simulations (2013), Department of Applied Mathematics and Computer Science, Technical University of Denmark.
- Kontos, S. Robust Numerical Methods for Nonlinear Wave-Structure Interaction in a Moving Frame of Reference (2016), Department of Mechanical Engineering/Department of Applied Mathematics and Computer Science/FORCE Technology, Technical University of Denmark.
- Bosi, U. A unified spectral/hp element depth-integrated Boussinesq model for nonlinear wave-floating body interaction (2019), INRIA / RISE / DTU Compute.
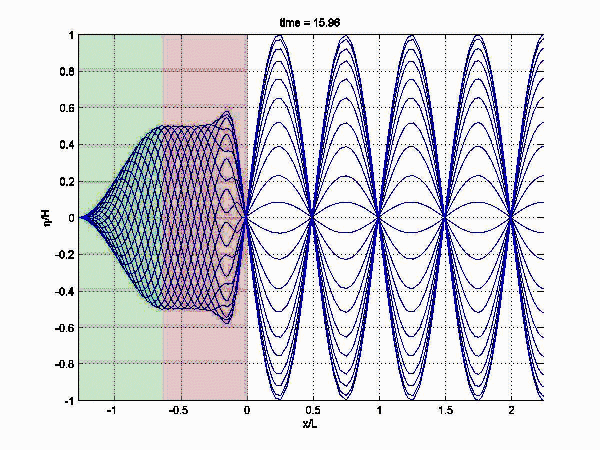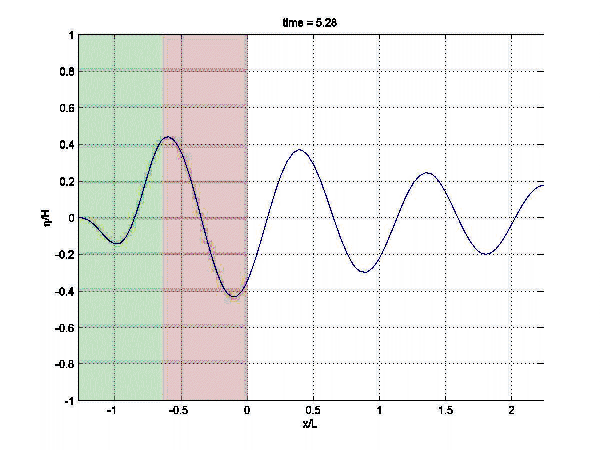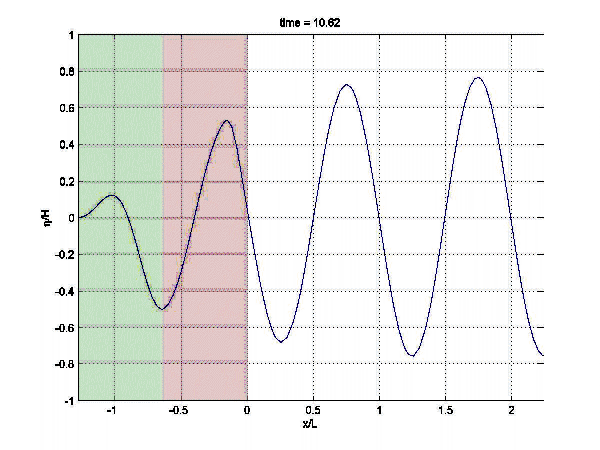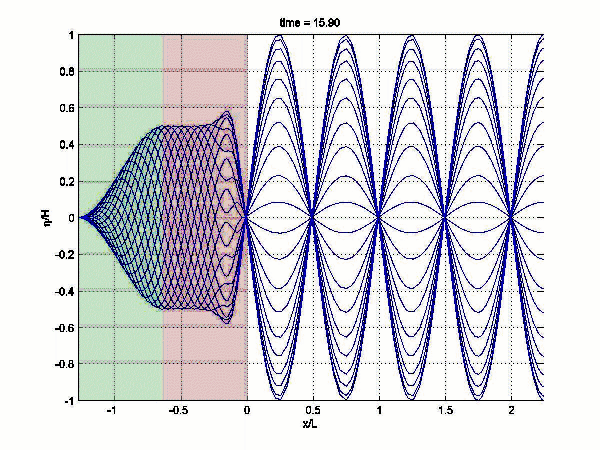
Data
 |  |
